- Appendices
- Miscellaneous
- External Links
Expected return calculator Blackjack Video Poker Roulette Craps Other Games: 3-L Other Games: M-Z.
Introduction
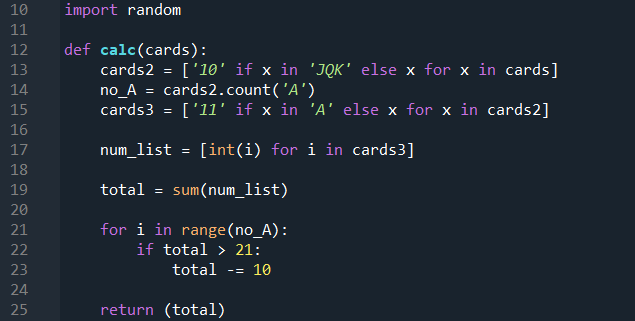
- This calculator allows you to determine the Playing Efficiency (PE), Betting Correlation (BC) and Insurance Correlation (IC) of any card counting system. Just plug in the tag values for each card rank and click Calculate. For example, for the popular Hi-Lo counting system, you would input the tag value -1 for Ace and Ten, and tag value +1 for 2-6.
- Colin is the founder of Blackjack Apprenticeship. Colin has been counting cards for over 15 years, and ran a multi-million dollar blackjack team. You may have seen his team featured in the documentary Holy Rollers: The True Story of Card Counting Christians, and has been covered by New York Times, CNN, and The Colbert Report.
The following tables display expected returns for any play in blackjack based on the following rules: dealer stands on a soft 17, an infinite deck, the player may double after a split, split up to three times except for aces, and draw only one card to split aces. Based on these rules, the player's expected value is -0.511734%.
To use this table, look up the returns for any given play, the one with the greatest return is the best play. For example suppose you have two 8's and the dealer has a 10. The return by standing is -0.5404, by hitting is -0.5398, doubling is -1.0797, and by splitting is -0.4807. So splitting 8's you stand to lose the least, 48.07 cents per original dollar bet, and is thus the best play.
Stand
Player's Expected Return by StandingExpand
| Player's Hand | Dealer's Up Card | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Ace | |
| 0-16 | -0.292784 | -0.252250 | -0.211063 | -0.167193 | -0.153699 | -0.475375 | -0.510518 | -0.543150 | -0.540430 | -0.666951 |
| 17 | -0.152975 | -0.117216 | -0.080573 | -0.044941 | 0.011739 | -0.106809 | -0.381951 | -0.423154 | -0.419721 | -0.478033 |
| 18 | 0.121742 | 0.148300 | 0.175854 | 0.199561 | 0.283444 | 0.399554 | 0.105951 | -0.183163 | -0.178301 | -0.100199 |
| 19 | 0.386305 | 0.404363 | 0.423179 | 0.439512 | 0.495977 | 0.615976 | 0.593854 | 0.287597 | 0.063118 | 0.277636 |
| 20 | 0.639987 | 0.650272 | 0.661050 | 0.670360 | 0.703959 | 0.773227 | 0.791815 | 0.758357 | 0.554538 | 0.655470 |
| 21 | 0.882007 | 0.885300 | 0.888767 | 0.891754 | 0.902837 | 0.925926 | 0.930605 | 0.939176 | 0.962624 | 0.922194 |
Hit
Player's Expected Return by HittingExpand
| Player's Hand | Dealer's Up Card | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Ace | |
| 4 | -0.114913 | -0.082613 | -0.049367 | -0.012380 | 0.011130 | -0.088279 | -0.159334 | -0.240666 | -0.289198 | -0.253077 |
| 5 | -0.128216 | -0.095310 | -0.061479 | -0.023979 | -0.001186 | -0.119447 | -0.188093 | -0.266615 | -0.313412 | -0.278575 |
| 6 | -0.140759 | -0.107291 | -0.072917 | -0.034916 | -0.013006 | -0.151933 | -0.217242 | -0.292641 | -0.337749 | -0.304147 |
| 7 | -0.109183 | -0.076583 | -0.043022 | -0.007271 | 0.029185 | -0.068808 | -0.210605 | -0.285365 | -0.319055 | -0.310072 |
| 8 | -0.021798 | 0.008005 | 0.038784 | 0.070805 | 0.114960 | 0.082207 | -0.059898 | -0.210186 | -0.249375 | -0.197029 |
| 9 | 0.074446 | 0.101265 | 0.128981 | 0.158032 | 0.196019 | 0.171868 | 0.098376 | -0.052178 | -0.152953 | -0.065681 |
| 10 | 0.182500 | 0.206088 | 0.230470 | 0.256259 | 0.287795 | 0.256909 | 0.197954 | 0.116530 | 0.025309 | 0.081450 |
| 11 | 0.238351 | 0.260325 | 0.283020 | 0.307350 | 0.333690 | 0.292147 | 0.229982 | 0.158257 | 0.119482 | 0.143001 |
| 12 | -0.253390 | -0.233691 | -0.213537 | -0.193271 | -0.170526 | -0.212848 | -0.271575 | -0.340013 | -0.381043 | -0.350540 |
| 13 | -0.307791 | -0.291210 | -0.274224 | -0.257333 | -0.235626 | -0.269073 | -0.323605 | -0.387155 | -0.425254 | -0.396930 |
| 14 | -0.362192 | -0.348729 | -0.334911 | -0.321395 | -0.300726 | -0.321282 | -0.371919 | -0.430930 | -0.466307 | -0.440007 |
| 15 | -0.416594 | -0.406249 | -0.395599 | -0.385457 | -0.365826 | -0.369762 | -0.416782 | -0.471578 | -0.504428 | -0.480006 |
| 16 | -0.470995 | -0.463768 | -0.456286 | -0.449520 | -0.430927 | -0.414779 | -0.458440 | -0.509322 | -0.539826 | -0.517149 |
| 17 | -0.536151 | -0.531674 | -0.527011 | -0.522986 | -0.508753 | -0.483486 | -0.505983 | -0.553695 | -0.584463 | -0.557300 |
| 18 | -0.622439 | -0.620005 | -0.617462 | -0.615260 | -0.607479 | -0.591144 | -0.591056 | -0.616528 | -0.647671 | -0.626515 |
| 19 | -0.729077 | -0.728033 | -0.726937 | -0.725991 | -0.722554 | -0.715450 | -0.713660 | -0.715574 | -0.729449 | -0.724795 |
| 20 | -0.855230 | -0.854977 | -0.854710 | -0.854480 | -0.853628 | -0.851852 | -0.851492 | -0.850833 | -0.849029 | -0.852139 |
| Soft 12 | 0.081836 | 0.103507 | 0.126596 | 0.156482 | 0.185954 | 0.165473 | 0.095115 | 0.000066 | -0.070002 | -0.020478 |
| Soft 13 | 0.046636 | 0.074119 | 0.102477 | 0.133363 | 0.161693 | 0.122386 | 0.054057 | -0.037695 | -0.104851 | -0.057308 |
| Soft 14 | 0.022392 | 0.050807 | 0.080081 | 0.111894 | 0.139165 | 0.079507 | 0.013277 | -0.075163 | -0.139467 | -0.093874 |
| Soft 15 | -0.000121 | 0.029160 | 0.059285 | 0.091960 | 0.118246 | 0.037028 | -0.027055 | -0.112189 | -0.173704 | -0.130027 |
| Soft 16 | -0.021025 | 0.009059 | 0.039975 | 0.073449 | 0.098821 | -0.004890 | -0.066795 | -0.148644 | -0.207441 | -0.165637 |
| Soft 17 | -0.000491 | 0.028975 | 0.059326 | 0.091189 | 0.128052 | 0.053823 | -0.072915 | -0.149787 | -0.196867 | -0.179569 |
| Soft 18 | 0.062905 | 0.090248 | 0.118502 | 0.147613 | 0.190753 | 0.170676 | 0.039677 | -0.100744 | -0.143808 | -0.092935 |
| Soft 19 | 0.123958 | 0.149340 | 0.175577 | 0.202986 | 0.239799 | 0.220620 | 0.152270 | 0.007893 | -0.088096 | -0.005743 |
| Soft 20 | 0.182500 | 0.206088 | 0.230470 | 0.256259 | 0.287795 | 0.256909 | 0.197954 | 0.116530 | 0.025309 | 0.081450 |
| Soft 21 | 0.238351 | 0.260325 | 0.283020 | 0.307350 | 0.333690 | 0.292147 | 0.229982 | 0.158257 | 0.119482 | 0.143001 |
Double
Player's Expected Return by DoublingExpand
| Player's Hand | Dealer's Up Card | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Ace | |
| Hard 4 | -0.585567 | -0.504500 | -0.422126 | -0.334385 | -0.307398 | -0.950750 | -1.021035 | -1.086299 | -1.080861 | -1.333902 |
| Hard 5 | -0.585567 | -0.504500 | -0.422126 | -0.334385 | -0.307398 | -0.950750 | -1.021035 | -1.086299 | -1.080861 | -1.333902 |
| Hard 6 | -0.564058 | -0.483726 | -0.402051 | -0.315577 | -0.281946 | -0.894048 | -1.001256 | -1.067839 | -1.062290 | -1.304837 |
| Hard 7 | -0.435758 | -0.359779 | -0.282299 | -0.202730 | -0.138337 | -0.589336 | -0.847076 | -0.957074 | -0.950866 | -1.130452 |
| Hard 8 | -0.204491 | -0.136216 | -0.066372 | 0.003456 | 0.087015 | -0.187730 | -0.451987 | -0.718501 | -0.746588 | -0.810746 |
| Hard 9 | 0.061119 | 0.120816 | 0.181949 | 0.243057 | 0.317055 | 0.104250 | -0.026442 | -0.300996 | -0.466707 | -0.432911 |
| Hard 10 | 0.358939 | 0.409321 | 0.460940 | 0.512517 | 0.575590 | 0.392412 | 0.286636 | 0.144328 | -0.008659 | -0.014042 |
| Hard 11 | 0.470641 | 0.517795 | 0.566041 | 0.614699 | 0.667380 | 0.462889 | 0.350693 | 0.227783 | 0.179689 | 0.109061 |
| Hard 12 | -0.506780 | -0.467382 | -0.427073 | -0.386542 | -0.341052 | -0.506712 | -0.615661 | -0.737506 | -0.796841 | -0.829344 |
| Hard 13 | -0.615582 | -0.582420 | -0.548448 | -0.514667 | -0.471253 | -0.587423 | -0.690966 | -0.807790 | -0.867544 | -0.880582 |
| Hard 14 | -0.724385 | -0.697459 | -0.669823 | -0.642791 | -0.601453 | -0.668135 | -0.766271 | -0.878075 | -0.938247 | -0.931821 |
| Hard 15 | -0.833187 | -0.812497 | -0.791198 | -0.770915 | -0.731653 | -0.748846 | -0.841576 | -0.948360 | -1.008950 | -0.983059 |
| Hard 16 | -0.941990 | -0.927536 | -0.912573 | -0.899039 | -0.861853 | -0.829558 | -0.916881 | -1.018644 | -1.079653 | -1.034297 |
| Hard 17 | -1.072302 | -1.063348 | -1.054023 | -1.045971 | -1.017505 | -0.966972 | -1.011965 | -1.107390 | -1.168926 | -1.114600 |
| Hard 18 | -1.244877 | -1.240010 | -1.234924 | -1.230519 | -1.214958 | -1.182288 | -1.182112 | -1.233057 | -1.295342 | -1.253031 |
| Hard 19 | -1.458155 | -1.456066 | -1.453874 | -1.451983 | -1.445108 | -1.430899 | -1.427320 | -1.431149 | -1.458898 | -1.449590 |
| Hard 20 | -1.710461 | -1.709954 | -1.709420 | -1.708961 | -1.707256 | -1.703704 | -1.702984 | -1.701665 | -1.698058 | -1.704278 |
| Soft 12 | -0.071570 | -0.007228 | 0.058427 | 0.125954 | 0.179748 | -0.183866 | -0.314441 | -0.456367 | -0.514028 | -0.624391 |
| Soft 13 | -0.071570 | -0.007228 | 0.058427 | 0.125954 | 0.179748 | -0.183866 | -0.314441 | -0.456367 | -0.514028 | -0.624391 |
| Soft 14 | -0.071570 | -0.007228 | 0.058427 | 0.125954 | 0.179748 | -0.183866 | -0.314441 | -0.456367 | -0.514028 | -0.624391 |
| Soft 15 | -0.071570 | -0.007228 | 0.058427 | 0.125954 | 0.179748 | -0.183866 | -0.314441 | -0.456367 | -0.514028 | -0.624391 |
| Soft 16 | -0.071570 | -0.007228 | 0.058427 | 0.125954 | 0.179748 | -0.183866 | -0.314441 | -0.456367 | -0.514028 | -0.624391 |
| Soft 17 | -0.007043 | 0.055095 | 0.118653 | 0.182378 | 0.256104 | -0.013758 | -0.255102 | -0.400984 | -0.458316 | -0.537198 |
| Soft 18 | 0.119750 | 0.177641 | 0.237004 | 0.295225 | 0.381506 | 0.219948 | -0.029917 | -0.290219 | -0.346892 | -0.362813 |
| Soft 19 | 0.241855 | 0.295824 | 0.351154 | 0.405972 | 0.479599 | 0.319835 | 0.195269 | -0.072946 | -0.235468 | -0.188428 |
| Soft 20 | 0.358939 | 0.409321 | 0.460940 | 0.512517 | 0.575590 | 0.392412 | 0.286636 | 0.144328 | -0.008659 | -0.014042 |
| Soft 21 | 0.470641 | 0.517795 | 0.566041 | 0.614699 | 0.667380 | 0.462889 | 0.350693 | 0.227783 | 0.179689 | 0.109061 |
Split

Player's Expected Return by SplittingExpand
| Player's Hand | Dealer's Up Card | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Ace | |
| 2,2 | -0.084336 | -0.015650 | 0.059088 | 0.151665 | 0.226890 | 0.006743 | -0.176693 | -0.386883 | -0.507175 | -0.433570 |
| 3,3 | -0.137710 | -0.056273 | 0.029932 | 0.126284 | 0.201318 | -0.053043 | -0.231843 | -0.436607 | -0.553507 | -0.482405 |
| 4,4 | -0.192325 | -0.108712 | -0.020395 | 0.081913 | 0.151377 | -0.166452 | -0.326068 | -0.511152 | -0.625044 | -0.560206 |
| 5,5 | -0.290154 | -0.208718 | -0.119335 | -0.019231 | 0.045404 | -0.293928 | -0.454237 | -0.634113 | -0.729969 | -0.668811 |
| 6,6 | -0.212560 | -0.119715 | -0.021320 | 0.080912 | 0.153668 | -0.264427 | -0.425122 | -0.610576 | -0.716103 | -0.653362 |
| 7,7 | -0.131478 | -0.043733 | 0.049255 | 0.146678 | 0.247385 | -0.050148 | -0.391981 | -0.577584 | -0.657268 | -0.651641 |
| 8,8 | 0.073852 | 0.146187 | 0.220849 | 0.297475 | 0.409329 | 0.321042 | -0.022736 | -0.387228 | -0.480686 | -0.372535 |
| 9,9 | 0.195625 | 0.258548 | 0.323474 | 0.391987 | 0.471339 | 0.364837 | 0.234447 | -0.078010 | -0.317336 | -0.136810 |
| 10,10 | 0.134774 | 0.212836 | 0.293403 | 0.380367 | 0.468117 | 0.296633 | 0.064443 | -0.206733 | -0.371278 | -0.249494 |
| A,A | 0.470641 | 0.517795 | 0.566041 | 0.614699 | 0.667380 | 0.462889 | 0.350693 | 0.227783 | 0.179689 | 0.109061 |
Here are basic strategy tables for infinite decks.
The only differences between infinite and four decks is to hit soft 13 vs. 5, and soft 15 vs 4 only when the dealer stands on soft 17.
I have had a lot of requests for my actual spreadsheet through the years. It is available to the public at Google docs. Note that this document allows for infinite re-splitting, while the tables above are based on a maximum of three splits (except aces).
Written by: Michael Shackleford
When discussing some of the side bets in blackjack, you'll notice that I use terms like 'expected return' and 'house edge.' Here's an explanation of those concepts.
The expected return is the amount of money that you can expect to win or lose (in the long run) from each wager. For example, if you're placing an even-money $1 bet, and your chances are 40% fora win and 60% for a loss. This would give you the following: $0.40 – $0.60 = -$0.20. The negative sign in front of the total means that for every dollar wagered you can expect to lose $0.20 (onaverage, over a long period of time—in the short run, anything can happen).
Here's an example where you have multiple options for winning. Let's say that you're betting $1 on a slot machine, and you have a 20% chance of winning $4, a 25% chance of winning $3, and a 55%chance of losing. Here's how the expected return would be calculated:

20% x $4 = $0.80
25% x $3 = $0.75
55% x -$1 = -$0.55

Player's Expected Return by SplittingExpand
| Player's Hand | Dealer's Up Card | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Ace | |
| 2,2 | -0.084336 | -0.015650 | 0.059088 | 0.151665 | 0.226890 | 0.006743 | -0.176693 | -0.386883 | -0.507175 | -0.433570 |
| 3,3 | -0.137710 | -0.056273 | 0.029932 | 0.126284 | 0.201318 | -0.053043 | -0.231843 | -0.436607 | -0.553507 | -0.482405 |
| 4,4 | -0.192325 | -0.108712 | -0.020395 | 0.081913 | 0.151377 | -0.166452 | -0.326068 | -0.511152 | -0.625044 | -0.560206 |
| 5,5 | -0.290154 | -0.208718 | -0.119335 | -0.019231 | 0.045404 | -0.293928 | -0.454237 | -0.634113 | -0.729969 | -0.668811 |
| 6,6 | -0.212560 | -0.119715 | -0.021320 | 0.080912 | 0.153668 | -0.264427 | -0.425122 | -0.610576 | -0.716103 | -0.653362 |
| 7,7 | -0.131478 | -0.043733 | 0.049255 | 0.146678 | 0.247385 | -0.050148 | -0.391981 | -0.577584 | -0.657268 | -0.651641 |
| 8,8 | 0.073852 | 0.146187 | 0.220849 | 0.297475 | 0.409329 | 0.321042 | -0.022736 | -0.387228 | -0.480686 | -0.372535 |
| 9,9 | 0.195625 | 0.258548 | 0.323474 | 0.391987 | 0.471339 | 0.364837 | 0.234447 | -0.078010 | -0.317336 | -0.136810 |
| 10,10 | 0.134774 | 0.212836 | 0.293403 | 0.380367 | 0.468117 | 0.296633 | 0.064443 | -0.206733 | -0.371278 | -0.249494 |
| A,A | 0.470641 | 0.517795 | 0.566041 | 0.614699 | 0.667380 | 0.462889 | 0.350693 | 0.227783 | 0.179689 | 0.109061 |
Here are basic strategy tables for infinite decks.
The only differences between infinite and four decks is to hit soft 13 vs. 5, and soft 15 vs 4 only when the dealer stands on soft 17.
I have had a lot of requests for my actual spreadsheet through the years. It is available to the public at Google docs. Note that this document allows for infinite re-splitting, while the tables above are based on a maximum of three splits (except aces).
Written by: Michael Shackleford
When discussing some of the side bets in blackjack, you'll notice that I use terms like 'expected return' and 'house edge.' Here's an explanation of those concepts.
The expected return is the amount of money that you can expect to win or lose (in the long run) from each wager. For example, if you're placing an even-money $1 bet, and your chances are 40% fora win and 60% for a loss. This would give you the following: $0.40 – $0.60 = -$0.20. The negative sign in front of the total means that for every dollar wagered you can expect to lose $0.20 (onaverage, over a long period of time—in the short run, anything can happen).
Here's an example where you have multiple options for winning. Let's say that you're betting $1 on a slot machine, and you have a 20% chance of winning $4, a 25% chance of winning $3, and a 55%chance of losing. Here's how the expected return would be calculated:
20% x $4 = $0.80
25% x $3 = $0.75
55% x -$1 = -$0.55
Blackjack Return Calculator Online
$0.80 + $0.75 – $0.55 = $1
In this example, you could expect to win $1 per spin over the long term. Of course, no sane casino ever offers a slot machine game with a positive return.
The house edge, meanwhile, is the ratio of the average loss to the initial bet. Expressed as a percentage, this number demonstrates the subtle way in which casino games bleed aplayer dry.
For example, a 5% house edge means you can expect to lose $5 for every $100 wagered—or $0.05 for every $1. This might not sound like a lot, but it gives the casino a financial advantage over theplayer and allows for a steady accumulation of profit.
Blackjack Probability Calculator
Game designers and casinos carefully calculate the expected return and house edge before putting a game on the casino floor. The end result is that the house almost always has an advantage overthe player, which explains why the major casinos rake in obscene amounts of money on an annual basis.

